Offset Curve 簡單的例子,如下是函數型的Offset Curve: y= Offset +Sin[x]

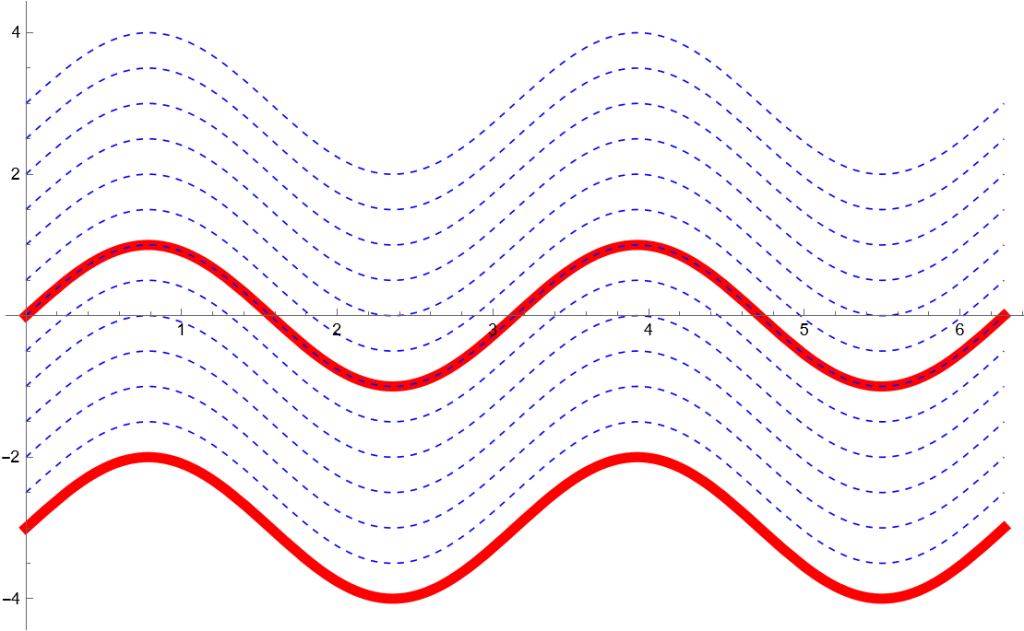
如果不是函數就比較麻煩一點.

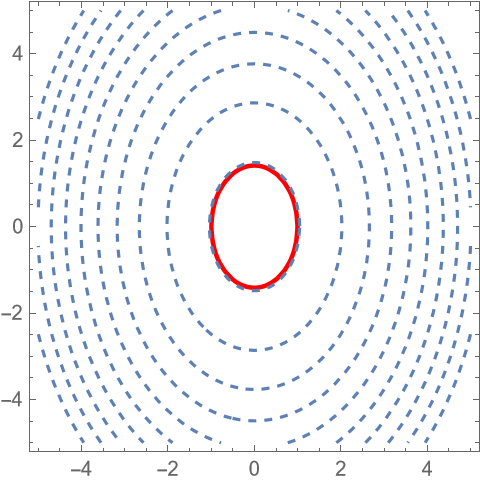
我示範這個題目: 有場V(x,y,z),且V(x,y,z)=定值的粉紅粗線，試畫出他的平行線(Offset Curve)

這個題目是活用求解Target Surface的理論。下圖虛線是粉紅粗線的平行線,觀察Pn各點，可知Offset Curve垂直於粉紅線.

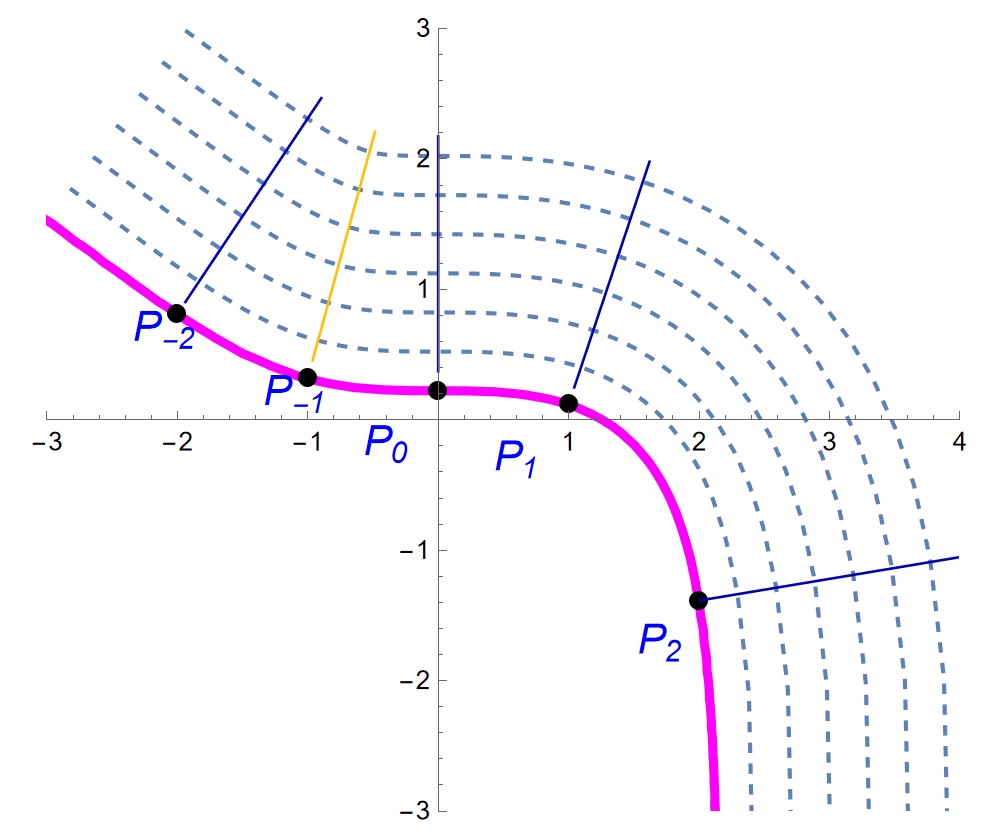
演算法,先求V場的梯度單位向量NormalUnitVector,將其延伸K倍,Pn+NormalUnitVector 得到一個對應點，之後用繪圖把Offset Curve描出來。

程式碼如下

(*From  https://qhand.work/2023/08/14/offset-curve/  *)(*Wolfram Mathematica \
Code V13.3 instal see:https://qhand.work/2022/07/30/install/*)
ClearAll["`*"]
V[x_, z_] = 8 E^z + x^3;
\[Del]V = \!\(
\*SubscriptBox[\(\[Del]\), \({x, z}\)]\(V[x, z]\)\);
NormalUnitVector[x_, z_] = \[Del]V // Normalize // N;
equalPointXZ[x0_] := 
  SolveValues[V[x, z] == 10 && x == x0, {x, z}, Reals][[1]] // N // 
   Quiet;
NormalkTimeEqualPointXZ[x0_, k_] := 
  equalPointXZ[x0] + {k, k}*NormalUnitVector @@ equalPointXZ[x0] // N;
equalline = 
  ContourPlot[V[x, z] == 10, {x, -3, 3}, {z, -3, 3}, 
   AxesLabel -> Automatic, AspectRatio -> Automatic, 
   ContourStyle -> Directive[Thickness[0.01], Magenta], 
   ContourLabels -> True];
OffsetCurves = 
  ParallelMap[
   ParametricPlot[NormalkTimeEqualPointXZ[x0, #], {x0, -3, 3}, 
     PlotPoints -> 10, MaxRecursion -> 3, PlotStyle -> Dashed, 
     PlotRange -> {{-3, 4}, {-3, 3}}] &, Range[0, 2, 0.3]];
Subscript[P, -2] = 
  Graphics[{PointSize[Large], Black, Point[equalPointXZ[-2]], 
    Text[Style["\!\(\*SubscriptBox[\(P\), \(-2\)]\)", Blue, Italic, 
      16], equalPointXZ[-2] - 0.1 {1, 1}] }];
Subscript[P, -1] = 
  Graphics[{PointSize[Large], Black, Point[equalPointXZ[-1]], 
    Text[Style["\!\(\*SubscriptBox[\(P\), \(-1\)]\)", Blue, Italic, 
      16], equalPointXZ[-1] - 0.1 {1, 1}] }];
Subscript[P, 0] = 
  Graphics[{PointSize[Large], Black, Point[equalPointXZ[0]], 
    Text[Style["\!\(\*SubscriptBox[\(P\), \(0\)]\)", Blue, Italic, 
      16], equalPointXZ[0] - 0.4 {1, 1}] }];
Subscript[P, 1] = 
  Graphics[{PointSize[Large], Black, Point[equalPointXZ[1]], 
    Text[Style["\!\(\*SubscriptBox[\(P\), \(1\)]\)", Blue, Italic, 
      16], equalPointXZ[1] - 0.4 {1, 1}] }];
Subscript[P, 2] = 
  Graphics[{PointSize[Large], Black, Point[equalPointXZ[2]], 
    Text[Style["\!\(\*SubscriptBox[\(P\), \(2\)]\)", Blue, Italic, 
      16], equalPointXZ[2] - 0.3 {1, 1}] }];
vectorPoints = {equalPointXZ[-2], equalPointXZ[-1], equalPointXZ[0], 
   equalPointXZ[1], equalPointXZ[2]};
vector = 
  VectorPlot[NormalUnitVector[x, z], {x, -3, 4}, {z, -3, 3}, 
   VectorMarkers -> Placed["Segment", "Start"], 
   VectorPoints -> vectorPoints, VectorSizes -> 3];
Show[OffsetCurves, equalline, Subscript[P, -2], Subscript[P, -1], \
Subscript[P, 0], Subscript[P, 1], Subscript[P, 2], vector]
ClearAll["`*"]
V[x_, z_] = 8 E^z + x^3;
\[Del]V = \!\(
\*SubscriptBox[\(\[Del]\), \({x, z}\)]\(V[x, z]\)\);
NormalUnitVector[x_, z_] = \[Del]V // Normalize // N;
equalPointXZ[x0_] := 
  SolveValues[V[x, z] == 10 && x == x0, {x, z}, Reals][[1]] // N // 
   Quiet;
NormalkTimeEqualPointXZ[x0_, k_] := 
  equalPointXZ[x0] + {k, k}*NormalUnitVector @@ equalPointXZ[x0] // N;
equalline = 
  ContourPlot[V[x, z] == 10, {x, -3, 3}, {z, -3, 3}, 
   AxesLabel -> Automatic, AspectRatio -> Automatic, 
   ContourStyle -> Directive[Thickness[0.01], Magenta], 
   ContourLabels -> True];
OffsetCurves = 
  ParallelMap[
   ParametricPlot[NormalkTimeEqualPointXZ[x0, #], {x0, -3, 3}, 
     PlotPoints -> 10, MaxRecursion -> 3, PlotStyle -> Dashed, 
     PlotRange -> {{-3, 4}, {-3, 3}}] &, Range[0, 2, 0.3]];
Subscript[P, -2] = 
  Graphics[{PointSize[Large], Black, Point[equalPointXZ[-2]], 
    Text[Style["\!\(\*SubscriptBox[\(P\), \(-2\)]\)", Blue, Italic, 
      16], equalPointXZ[-2] - 0.1 {1, 1}] }];
Subscript[P, -1] = 
  Graphics[{PointSize[Large], Black, Point[equalPointXZ[-1]], 
    Text[Style["\!\(\*SubscriptBox[\(P\), \(-1\)]\)", Blue, Italic, 
      16], equalPointXZ[-1] - 0.1 {1, 1}] }];
Subscript[P, 0] = 
  Graphics[{PointSize[Large], Black, Point[equalPointXZ[0]], 
    Text[Style["\!\(\*SubscriptBox[\(P\), \(0\)]\)", Blue, Italic, 
      16], equalPointXZ[0] - 0.4 {1, 1}] }];
Subscript[P, 1] = 
  Graphics[{PointSize[Large], Black, Point[equalPointXZ[1]], 
    Text[Style["\!\(\*SubscriptBox[\(P\), \(1\)]\)", Blue, Italic, 
      16], equalPointXZ[1] - 0.4 {1, 1}] }];
Subscript[P, 2] = 
  Graphics[{PointSize[Large], Black, Point[equalPointXZ[2]], 
    Text[Style["\!\(\*SubscriptBox[\(P\), \(2\)]\)", Blue, Italic, 
      16], equalPointXZ[2] - 0.3 {1, 1}] }];
vectorPoints = {equalPointXZ[-2], equalPointXZ[-1], equalPointXZ[0], 
   equalPointXZ[1], equalPointXZ[2]};
vector = 
  VectorPlot[NormalUnitVector[x, z], {x, -3, 4}, {z, -3, 3}, 
   VectorMarkers -> Placed["Segment", "Start"], 
   VectorPoints -> vectorPoints, VectorSizes -> 3];
Show[OffsetCurves, equalline, Subscript[P, -2], Subscript[P, -1], \
Subscript[P, 0], Subscript[P, 1], Subscript[P, 2], vector]