向大師致敬.復刻經典!!
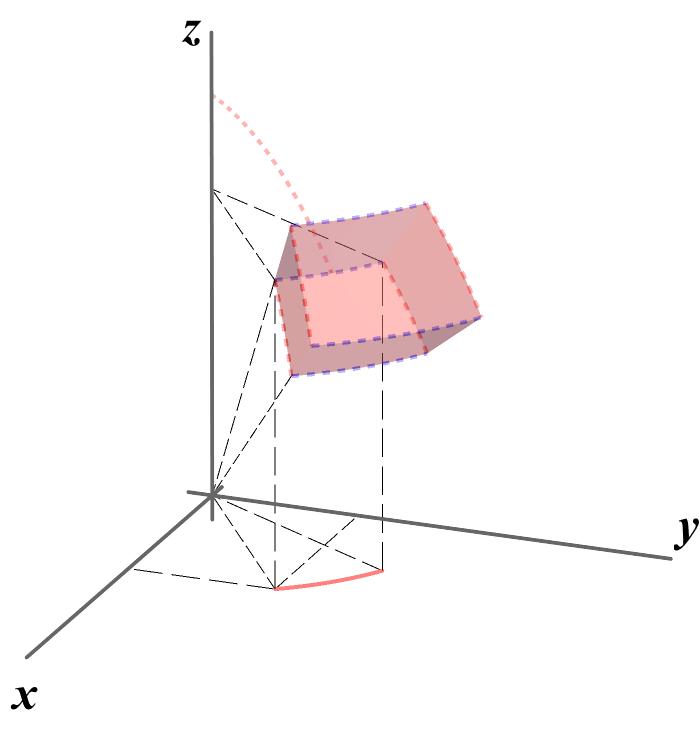
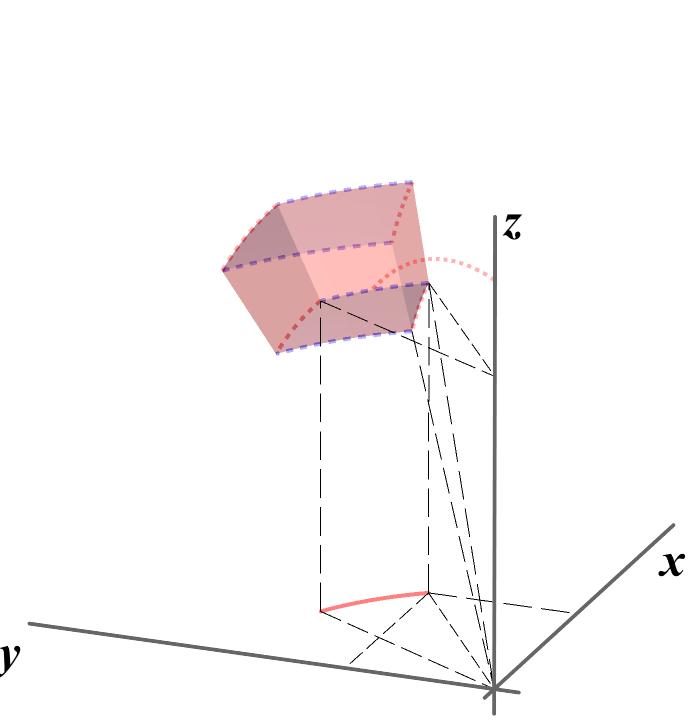
回想起以前教授很賣力在黑板講解這些球座標圖,幾乎要把黑板挖一個洞.加上自己只有大猩猩的智慧,根本就"轉不過來".坐標變換過節怎麼讀?想像看說明書駕駛太空梭,又沒有太空梭可以摸.其實這章節不難,因出場的符號太多,認識他們是很乏味很無聊的差事,眼花撩亂,硬讀會想睡.當我寫程式要復刻一下經典,發現大師要用這張球座標圖交待的事情太多,
下圖(執行我的code),把這章節變成虛擬太空梭,輔助你感覺圖上每條虛線,拉近你與大師的距離.
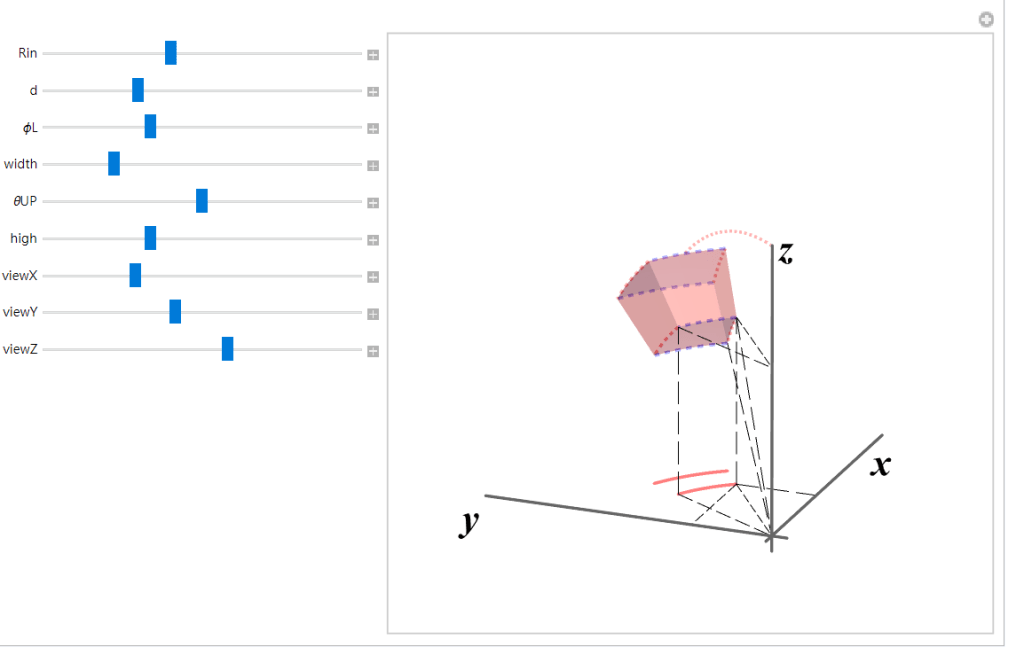
(*From https://qhand.work/2022/07/15/vector/ *)
(* Wolfram Mathematica Code V13.3 instal see: \
https://qhand.work/2022/07/30/install/*)
ClearAll["`*"]
trans = CoordinateTransformData["Spherical" -> "Cartesian", "Mapping"];
Manipulate[
Subscript[R, inner] = Rin;
Subscript[R, outter] = Rin + d;
Subscript[\[Phi], L] = \[Phi]L;
Subscript[\[Phi], R] = Subscript[\[Phi], L] + width;
Subscript[\[Theta], upper] = \[Theta]UP;
Subscript[\[Theta], down] = Subscript[\[Theta], upper] + high;
trans =
CoordinateTransformData["Spherical" -> "Cartesian", "Mapping"];
\!\(\*OverscriptBox[
SubscriptBox[\(O2\[Theta]\), \(upper\)], \(_\)]\) = Line[{
{trans@{Subscript[R, inner], Subscript[\[Theta], upper],
Subscript[\[Phi], L]}, {0, 0, 0}},
{trans@{Subscript[R, inner], Subscript[\[Theta], down],
Subscript[\[Phi], L]}, {0, 0, 0}}}
];
\!\(\*OverscriptBox[
SubscriptBox[\(zV\[Theta]\), \(upper\)], \(_\)]\) = Line[{
{trans@{Subscript[R, inner], Subscript[\[Theta], upper],
Subscript[\[Phi], L]},
trans@{Cos[Subscript[\[Theta], upper]] Subscript[R, inner], 0,
0}},
{trans@{Subscript[R, inner], Subscript[\[Theta], upper],
Subscript[\[Phi], R]},
trans@{Cos[Subscript[\[Theta], upper]] Subscript[R, inner], 0,
0}}}];
(*Overscript[Subscript[R\[Theta], upper], _]=Line[{
(*{trans@{Subscript[R, inner],Subscript[\[Theta], upper],Subscript[\
\[Phi], L]},trans@{Subscript[R, inner],0,0}},*)
{trans@{Subscript[R, inner],Subscript[\[Theta], upper],Subscript[\
\[Phi], R]},trans@{Subscript[R, inner],0,0}}}];*)
\!\(\*OverscriptBox[
SubscriptBox[\(zPP\[Theta]\), \(upper\)], \(_\)]\) = Line[{
{trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], L]},
trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], L]} +
trans@{Cos[Subscript[\[Theta], upper]] Subscript[R, inner], 0,
0}},
{trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], R]},
trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], R]} +
trans@{Cos[Subscript[\[Theta], upper]] Subscript[R, inner], 0,
0}}}];
\!\(\*OverscriptBox[
SubscriptBox[\(OXY\[Theta]\), \(upper\)], \(_\)]\) = Line[{
{trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], L]}, {0, 0, 0}},
{trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], R]}, {0, 0, 0}}}];
\!\(\*OverscriptBox[
SubscriptBox[\(OX\[Theta]\), \(upper\)], \(_\)]\) = Line[
{trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi],
L]}, {(trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], L]})[[1]], 0, 0}}];
\!\(\*OverscriptBox[
SubscriptBox[\(OY\[Theta]\), \(upper\)], \(_\)]\) = Line[
{trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi],
L]}, {0, (trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], L]})[[2]], 0}}];
\!\(\*OverscriptBox[
SubscriptBox[\(zPP\[Theta]\), \(upper\)], \(_\)]\) = Line[{
{trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], L]},
trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], L]} +
trans@{Cos[Subscript[\[Theta], upper]] Subscript[R, inner], 0,
0}},
{trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], R]},
trans@{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner], \[Pi]/2, Subscript[\[Phi], R]} +
trans@{Cos[Subscript[\[Theta], upper]] Subscript[R, inner], 0,
0}}}];
apt = (35 + 3.5);
axiresarrowheads = {Arrowheads[.08],
Arrow[{{0, 0, 0}, {apt, 0, 0}}],
Arrow[{{0, 0, 0}, {0, apt, 0}}],
Arrow[{{0, 0, 0}, {0, 0, apt}}]
};
AllDashLine = {Dashing[{0.044, 0.014`}],
\!\(\*OverscriptBox[
SubscriptBox[\(O2\[Theta]\), \(upper\)], \(_\)]\),
\!\(\*OverscriptBox[
SubscriptBox[\(zV\[Theta]\), \(upper\)], \(_\)]\),
\!\(\*OverscriptBox[
SubscriptBox[\(OXY\[Theta]\), \(upper\)], \(_\)]\),
\!\(\*OverscriptBox[
SubscriptBox[\(zPP\[Theta]\), \(upper\)], \(_\)]\) ,
\!\(\*OverscriptBox[
SubscriptBox[\(OX\[Theta]\), \(upper\)], \(_\)]\) ,
\!\(\*OverscriptBox[
SubscriptBox[\(OY\[Theta]\), \(upper\)], \(_\)]\)(*,
axiresarrowheads*)} // Graphics3D;
\[Theta]Curve = ParametricPlot3D[
Subscript[R,
outter] {
Sin[\[Theta]] Cos[(Subscript[\[Phi], L] + Subscript[\[Phi], R])/
2], Sin[\[Theta]] Sin[(
Subscript[\[Phi], L] + Subscript[\[Phi], R])/2] ,
Cos[\[Theta]]}, {\[Theta], 0, Subscript[\[Theta], upper]},
Mesh -> None, PlotStyle -> Directive[Red, Opacity[0.3], Dashed]];
d\[Phi]Project =
ParametricPlot3D[{Sin[Subscript[\[Theta], upper]] Subscript[R,
inner] {Cos[u], Sin[u], 0},
Sin[Subscript[\[Theta], down]] Subscript[R,
inner] {Cos[u], Sin[u], 0}}, {u, Subscript[\[Phi], L],
Subscript[\[Phi], R]}, PlotStyle -> Pink];
inoutSide = ParametricPlot3D[{
Subscript[R,
inner] { Sin[\[Theta]] Cos[\[Phi]], Sin[\[Theta]] Sin[\[Phi]] ,
Cos[\[Theta]]},
Subscript[R,
outter] { Sin[\[Theta]] Cos[\[Phi]], Sin[\[Theta]] Sin[\[Phi]] ,
Cos[\[Theta]]}}, {\[Theta], Subscript[\[Theta], upper],
Subscript[\[Theta], down]}, {\[Phi], Subscript[\[Phi], L],
Subscript[\[Phi], R]}, Mesh -> None,
PlotStyle -> Directive[Pink, Opacity[0.3]]];
updownSide = ParametricPlot3D[{
R*{ Sin[Subscript[\[Theta], upper]] Cos[\[Phi]],
Sin[Subscript[\[Theta], upper]] Sin[\[Phi]] ,
Cos[Subscript[\[Theta], upper]]},
R*{ Sin[Subscript[\[Theta], down]] Cos[\[Phi]],
Sin[Subscript[\[Theta], down]] Sin[\[Phi]] ,
Cos[Subscript[\[Theta], down]]}}, {R, Subscript[R, inner],
Subscript[R, outter]}, {\[Phi], Subscript[\[Phi], L],
Subscript[\[Phi], R]}, Mesh -> None,
PlotStyle -> Directive[Pink, Opacity[0.3]]];
RLSide = ParametricPlot3D[Evaluate@{
R*{ Sin[\[Theta]] Cos[Subscript[\[Phi], L]],
Sin[\[Theta]] Sin[Subscript[\[Phi], L]] , Cos[\[Theta]]},
R*{ Sin[\[Theta]] Cos[Subscript[\[Phi], R]],
Sin[\[Theta]] Sin[Subscript[\[Phi], R]] , Cos[\[Theta]]}}, {R,
Subscript[R, inner], Subscript[R, outter]}, {\[Theta],
Subscript[\[Theta], upper], Subscript[\[Theta], down]},
Mesh -> None, PlotStyle -> Directive[Pink, Opacity[0.3]]];
updownLine = ParametricPlot3D[{
Subscript[R,
inner] { Sin[Subscript[\[Theta], upper]] Cos[\[Phi]],
Sin[Subscript[\[Theta], upper]] Sin[\[Phi]] ,
Cos[Subscript[\[Theta], upper]]},
Subscript[R,
inner] { Sin[Subscript[\[Theta], down]] Cos[\[Phi]],
Sin[Subscript[\[Theta], down]] Sin[\[Phi]] ,
Cos[Subscript[\[Theta], down]]},
Subscript[R,
outter] { Sin[Subscript[\[Theta], upper]] Cos[\[Phi]],
Sin[Subscript[\[Theta], upper]] Sin[\[Phi]] ,
Cos[Subscript[\[Theta], upper]]},
Subscript[R,
outter] { Sin[Subscript[\[Theta], down]] Cos[\[Phi]],
Sin[Subscript[\[Theta], down]] Sin[\[Phi]] ,
Cos[Subscript[\[Theta], down]]}}, {\[Phi], Subscript[\[Phi], L],
Subscript[\[Phi], R]}, Mesh -> None,
PlotStyle -> Directive[Blue, Opacity[0.3], Dashed]];
RLLine = ParametricPlot3D[{
Subscript[R,
inner] { Sin[\[Theta]] Cos[Subscript[\[Phi], L]],
Sin[\[Theta]] Sin[Subscript[\[Phi], L]] , Cos[\[Theta]]},
Subscript[R,
inner] { Sin[\[Theta]] Cos[Subscript[\[Phi], R]],
Sin[\[Theta]] Sin[Subscript[\[Phi], R]] , Cos[\[Theta]]},
Subscript[R,
outter] { Sin[\[Theta]] Cos[Subscript[\[Phi], L]],
Sin[\[Theta]] Sin[Subscript[\[Phi], L]] , Cos[\[Theta]]},
Subscript[R,
outter] { Sin[\[Theta]] Cos[Subscript[\[Phi], R]],
Sin[\[Theta]] Sin[Subscript[\[Phi], R]] ,
Cos[\[Theta]]}}, {\[Theta], Subscript[\[Theta], upper],
Subscript[\[Theta], down]}, Mesh -> None,
PlotStyle -> Directive[Red, Opacity[0.3], Dashed]];
final =
Show[d\[Phi]Project, AllDashLine, inoutSide, updownSide, RLSide,
updownLine, RLLine, \[Theta]Curve,
PlotRange -> {{0.0001, 40}, {0.0001, 40}, {0.0001, 40}},
Axes -> True, AxesOrigin -> {0, 0, 0}, AxesStyle -> Thick,
AxesEdge -> {{-1, -1}, {-1, -1}, {-1, -1}}, Mesh -> None,
Ticks -> None, Boxed -> False,
AxesLabel -> {Style["x", Black, Large, Bold, Italic,
FontFamily -> "Times New Roman"],
Style["y", Black, Bold, Large, Italic,
FontFamily -> "Times New Roman"],
Style["z", Black, Bold, Large, Italic,
FontFamily -> "Times New Roman"]},
ViewPoint -> {viewX, viewY, viewZ}, ImageSize -> 350] ,
{{Rin, 32}, 20, 50},
{{d, 8}, 4, 25},
{{\[Phi]L, 35 °}, 25 °, 55 °},
{{width, 25 °}, 10 °, 80 °},
{{\[Theta]UP, 40 °}, 20 °, 60 °},
{{high, 14 °}, 4 °, 34 °},
{{viewX, -43}, -100, 100, 15},
{{viewY, -17}, -100, 100, 15},
{{viewZ, 17}, -100, 100, 15}]球座標相關應用,如下:
一. (柱座標)電場E=k r3 ar ,反求電荷密度

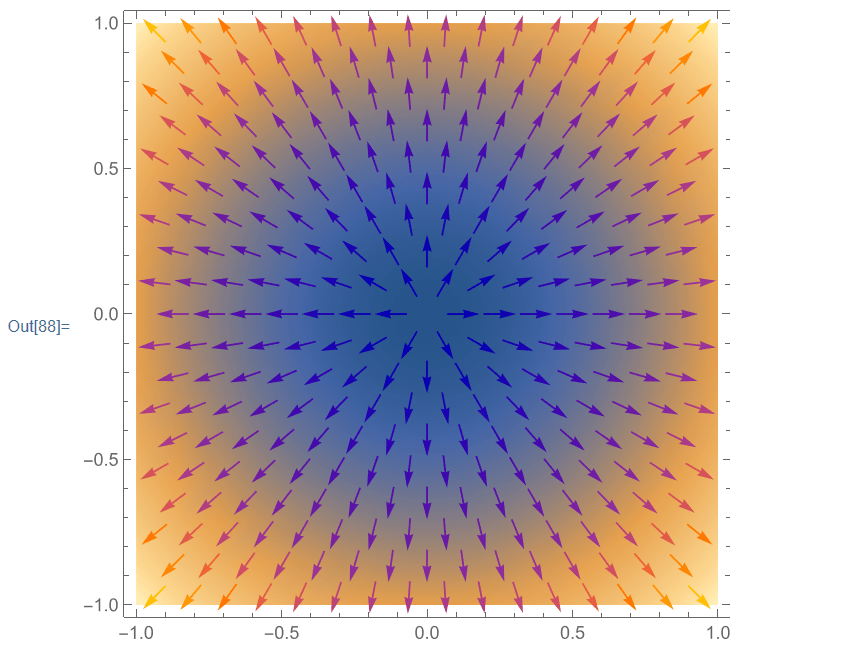
(*From https://qhand.work/2022/07/15/vector/ *)
(* Wolfram Mathematica Code V13.3 instal see: \
https://qhand.work/2022/07/30/install/*)
ClearAll["Global`*"];
field = {k*r^3, 0, 0};
diversionOfEfieldCyl = Div[field, {r, \[Theta], z}, "Cylindrical"]
4 k r^2
\[Rho]r = Solve[diversionOfEfieldCyl == \[Rho]/\[Epsilon], \[Rho]]
{{\[Rho] -> 4 k r^2 \[Epsilon]}}
fieldXYZ =
TransformedField["Cylindrical" -> "Cartesian",
field, {r, \[Theta], zc} -> {x, y, z}];
\[Rho]rToXYZ =
TransformedField[
"Cylindrical" ->
"Cartesian", \[Rho]r[[1, 1, 2]], {r, \[Theta], zz} -> {x, y, z}];
k = 1; \[Epsilon] = 1;
plot\[Rho]r = DensityPlot[\[Rho]rToXYZ, {x, -1, 1}, {y, -1, 1}];
vectorE = VectorPlot[fieldXYZ // Most, {x, -1, 1}, {y, -1, 1}];
Show[plot\[Rho]r, vectorE]
二. (改成球座標)電場E=k r3 ar ,再反求電荷密度

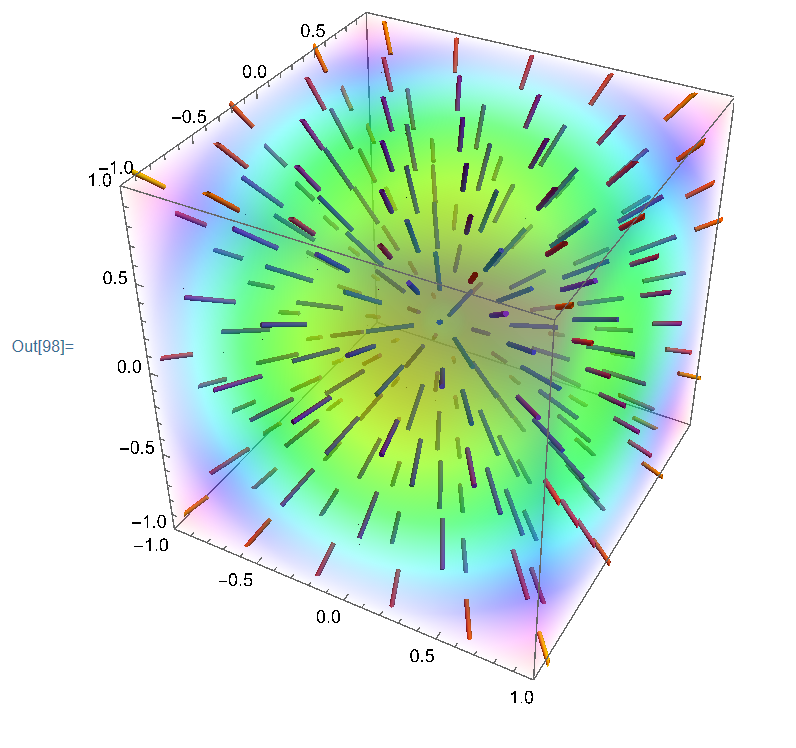
把我的程式碼,複製去執行看看.
(*From https://qhand.work/2022/07/15/vector/ *)
(* Wolfram Mathematica Code V13.3 instal see: \
https://qhand.work/2022/07/30/install/*)
ClearAll["Global`*"];
field = {k*R^3, 0, 0};
diversionOfEfieldSph = Div[field, {R, \[Theta], \[Phi]}, "Spherical"]
5 k R^2
\[Rho]R = Solve[diversionOfEfieldSph == \[Rho]/\[Epsilon], \[Rho]]
{{\[Rho] -> 5 k R^2 \[Epsilon]}}
EfieldSphToXYZ =
TransformedField["Spherical" -> "Cartesian",
field, {R, \[Theta], \[CurlyPhi]} -> {x, y, z}];
\[Rho]RToXYZ =
TransformedField[
"Spherical" ->
"Cartesian", \[Rho]R[[1, 1, 2]], {R, \[Theta], \[CurlyPhi]} -> {x,
y, z}];
k = 1; \[Epsilon] = 1;
plot\[Rho]R =
DensityPlot3D[\[Rho]RToXYZ, {x, -1, 1}, {y, -1, 1}, {z, -1, 1},
OpacityFunction -> 0.03, ColorFunction -> Hue];
vectorE3D =
VectorPlot3D[EfieldSphToXYZ, {x, -1, 1}, {y, -1, 1}, {z, -1, 1},
VectorMarkers -> "Tube", VectorSizes -> Small];
Show[plot\[Rho]R, vectorE3D]
(*StreamE=StreamPlot3D[EfieldSphToXYZ,{x,-1,1},{y,-1,1},{z,-1,1}];
Show[plot\[Rho]R,StreamE]*)
