Beginner 機器手臂運動學

On 由predliu撰寫In Mathematica

使用Wolfram Mathematica 完成 下列網站的機器運動學。

https://www.learnaboutrobots.com/forwardKinematics.htm

程式碼分享如下

COS[n_, \[Theta]_] := \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(n\)]\(Cos[i*\[Theta]]\)\)
SIN[n_, \[Theta]_] := \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(n\)]\(Sin[i*\[Theta]]\)\)
line[n_, \[Theta]_] := 
  N@Table[{ColorData[100, "ColorList"][[i]], 
        Line[{{COS[i - 1, \[Theta]], 
              SIN[i - 1, \[Theta]]}, {COS[i, \[Theta]], 
              SIN[i, \[Theta]]}}]}, {i, 1, n}]
Manipulate[
  Graphics[{Thickness[0.04], line[n, \[Theta]]}, 
    PlotRange -> {{-3, 10}, {-1, 5}}], {{\[Theta], 0.5}, 0, 
  1}, {{n, 4},
     3, 10, 1}, ControlPlacement -> Top]

另一個作法是用 Wolfram 本身的函數RotationTransform 來完成.

Manipulate[
 r = RotationTransform[\[Theta]];
 g = RotationTransform[\[Phi] + \[Theta]];
 h = RotationTransform[\[Phi] + \[Theta] + \[Tau]];
 mp = r[{1, 0}];
 vp = mp + g[{1, 0}];
 hp = vp + h[{1, 0}];
 Graphics[{Point[5 {{-1, -1}, {1, 1}}], 
   Line[{{0, 0}, mp, vp, hp}]}], {\[Theta], 0, 4 \[Pi]}, {\[Phi], 0, 
  4 \[Pi]}, {\[Tau], 0, 4 \[Pi]}]

再進一版,地球上最短的CODE


ClearAll["Global`*"]; 
n = 9;
ram = 0; rr = 
 Table[Subscript[l, i] = {2, 0}; ram += Subscript[\[Theta], i]; 
  Subscript[p, i] = RotationTransform[ram][Subscript[l, i]], {i, n}];
exp = Graphics@List@Line@FoldList[Plus[#1, #2] &, {0, 0}, rr];
ii = Prepend[
   Table[{Subscript[\[Theta], i], 0, (2 \[Pi])/(2 n)}, {i, n, 1, -1}],
    exp];
Manipulate @@ ii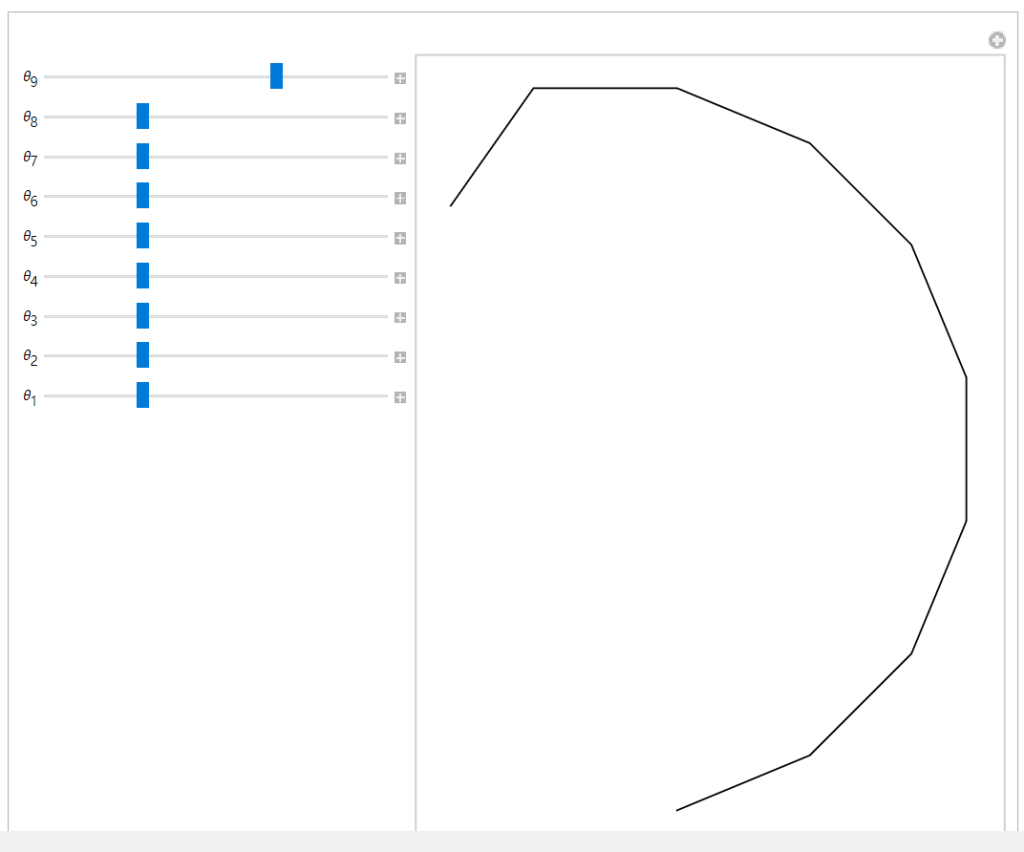

基本的弄懂之後,可以再做一些進階的控制,各位可以自由發運

參考資料

機器人建模和控制最最前面的內容

這個是前言裡的範例，用Wolfram入機器人的大門。

https://www.books.com.tw/products/CN11366996

發表留言