Building Optical Lens Imaging with Wolfram.If you’re learning to draw a light path diagram, Mathematica can help.

如果有光學相關的想法，無從驗證，Mathematica再次幫上忙，不然要從重新學一套軟體，只為驗證一個想法，就辛苦又耗錢。

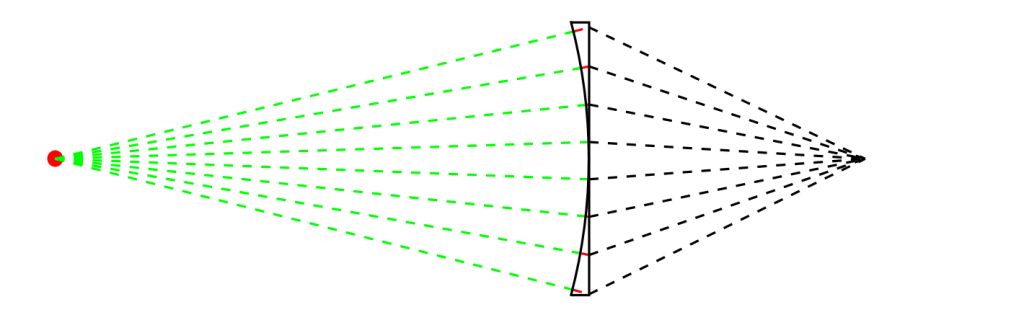
ClearAll["Global`*"];
monitorW = 1550; n = 2; r = 6000; distance = 2 monitorW;
n = 1.4; r = 6000; monitorW = 1550;
MaxAngle = SolveValues[monitorW == r*\[Theta], \[Theta]][[1]];

f[\[Gamma]_] := Block[{},
  LensW = r - r*Cos[\[Gamma]];
  LensH = r*Sin[\[Gamma]];
  AirH = distance*Tan[\[Alpha]];
  angle = Solve[LensH - AirH == Tan[\[Omega]]*LensW
          && Sin[\[Alpha]] == n*Sin[\[Omega]]
         , {\[Alpha], \[Omega]}] // Values // First // First // 
     Quiet // Tan;
  AirH = distance*Tan[angle];
  {
   Green, Dashed, Line[{{0, 0}, {r*Cos[\[Gamma]], LensH}}],
   Red, Line[{{r*Cos[\[Gamma]], LensH}, {r, AirH}}],
   Black, Line[{{r, AirH}, {r + distance, 0}}]
   }]

light = Table[
   f[(MaxAngle - k) // N], {k, 1 \[Degree], 2 MaxAngle, 4 \[Degree]}];

point = {PointSize[Large], Red, Point[{0, 0}]};
lens = {Circle[{0, 0}, r, {-MaxAngle, MaxAngle}],
   Line[{{r - LensW, -r*Sin[MaxAngle]}, {r, -r*Sin[MaxAngle]}, {r, 
      r*Sin[MaxAngle]}, {r - LensW, r*Sin[MaxAngle]}}]};
Graphics[{point, {light}, lens}]